已知抛物线 .
(1)通过配方可以将其化成顶点式为 ,根据该抛物线在对称轴两侧从左到右图象的特征,可以判断,当顶点在 轴 (填上方或下方),即 0(填大于或小于)时,该抛物线与 轴必有两个交点;
(2)若抛物线上存在两点 , , , ,分布在 轴的两侧,则抛物线顶点必在 轴下方,请你结合 、 两点在抛物线上的可能位置,根据二次函数的性质,对这个结论的正确性给以说明;(为了便于说明,不妨设 且都不等于顶点的横坐标;另如果需要借助图象辅助说明,可自己画出简单示意图)
(3)根据二次函数(1)(2)结论,求证:当 , 时, .
推荐套卷
 2
2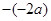 2
2 粤公网安备 44130202000953号
粤公网安备 44130202000953号