八(11)班同学到野外上数学活动课,为测量池塘两端A、B的距离,设计了如下方案:
(Ⅰ)如左图,先在平地上取一个可直接到达A、B的点C,连接AC、 BC,并分别延长AC至D,BC至E,使DC=AC,EC=BC,最后测出DE的距离即为AB的长;
(Ⅱ)如右图,先过B点作AB的垂线BF,再在BF上取C、D两点使BC=CD,接着过D作BD的垂线DE,交AC的延长线于E,则测出DE的长即为AB的距离.
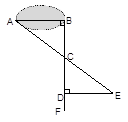
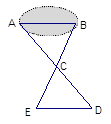
阅读后回答下列问题:
(1)方案(Ⅰ)是否可行?请说明理由。
(2)方案(Ⅱ)是否可行?请说明理由。
若仅满足∠ABD=∠BDE≠90°,方案(Ⅱ)是否成立?