问题提出:如何将边长为
,且
为整数)的正方形分割为一些
或
的矩形(
的矩形指边长分别为
,
的矩形)?
问题探究:我们先从简单的问题开始研究解决,再把复杂问题转化为已解决的问题.
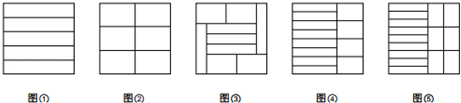
探究一:
如图①,当
时,可将正方形分割为五个
的矩形.
如图②,当
时,可将正方形分割为六个
的矩形.
如图③,当
时,可将正方形分割为五个
的矩形和四个
的矩形
如图④,当
时,可将正方形分割为八个
的矩形和四个
的矩形
如图⑤,当
时,可将正方形分割为九个
的矩形和六个
的矩形
探究二:
当
,11,12,13,14时,分别将正方形按下列方式分割:
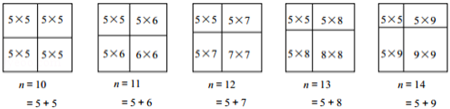
所以,当
,11,12,13,14时,均可将正方形分割为一个
的正方形、一个
的正方形和两个
的矩形.显然,
的正方形和
的矩形均可分割为
的矩形,而
的正方形是边长分别为5,6,7,8,9的正方形,用探究一的方法可分割为一些
或
的矩形.
探究三:
当
,16,17,18,19时,分别将正方形按下列方式分割:
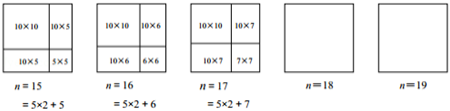
请按照上面的方法,分别画出边长为18,19的正方形分割示意图.
所以,当
,16,17,18,19时,均可将正方形分割为一个
的正方形、一个
的正方形和两个
的矩形.显然,
的正方形和
的矩形均可分割为
的矩形,而
的正方形又是边长分别为5,6,7,8,9的正方形,用探究一的方法可分割为一些
或
的矩形.
问题解决:如何将边长为
,且
为整数)的正方形分割为一些
或
的矩形?请按照上面的方法画出分割示意图,并加以说明.
实际应用:如何将边长为61的正方形分割为一些
或
的矩形?(只需按照探究三的方法画出分割示意图即可)