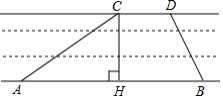
京杭大运河是世界文化遗产．综合实践活动小组为了测出某段运河的河宽（岸沿是平行的），如图，在岸边分别选定了点 、 和点 、 ，先用卷尺量得 ， ，再用测角仪测得 ， ，求该段运河的河宽（即 的长）．
·
，其中
．
；（2）sin30°+cos30°•tan60°．
（n为正整数）
相关知识点
推荐套卷
京杭大运河是世界文化遗产．综合实践活动小组为了测出某段运河的河宽（岸沿是平行的），如图，在岸边分别选定了点 、 和点 、 ，先用卷尺量得 ， ，再用测角仪测得 ， ，求该段运河的河宽（即 的长）．
粤公网安备 44130202000953号