传统的端午节即将来临，某企业接到一批粽子生产任务，约定这批粽子的出厂价为每只4元，按要求在20天内完成．为了按时完成任务，该企业招收了新工人，设新工人李明第 天生产的粽子数量为 只， 与 满足如下关系：
（1）李明第几天生产的粽子数量为280只？
（2）如图，设第 天生产的每只粽子的成本是 元， 与 之间的关系可用图中的函数图象来刻画．若李明第 天创造的利润为 元，求 与 之间的函数表达式，并求出第几天的利润最大？最大利润是多少元？（利润 出厂价 成本）
相关试题
已知反比例函数
（k为常数，k≠1）．
（1）其图象与正比例函数y＝x的图象的一个交点为P．若点P的纵坐标是2，求k的值；
（2）若在其图象的每一支上，y随x的增大而减小，求k的取值范围；
（3）若其图象的一支位于第二象限，在这一支上任取两点A（x1，y1），B（x2，y2），当y1＞y2时，试比较x1与x2的大小．
已知A（0，－6），B（－3，0），C（m，2）三点在同一直线上，试求出图象经过其中一点的反比例函数的解析式，并在图中画出其图象．（要求标出必要的点，可不写画法）
时，y的值．
．相关知识点
推荐套卷
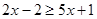
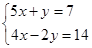
粤公网安备 44130202000953号