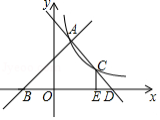
如图,一次函数 的图象与反比例函数 的图象相交于点 ,与 轴相交于点 .
(1)求这个反比例函数的表达式;
(2) 为反比例函数的图象上异于点 的一点,直线 交 轴于点 ,设直线 所对应的函数表达式为 .
①若 的面积为12,求 、 的值;
②作 轴,垂足为 ,记 ,求 的值.
相关知识点
推荐套卷
如图,一次函数 的图象与反比例函数 的图象相交于点 ,与 轴相交于点 .
(1)求这个反比例函数的表达式;
(2) 为反比例函数的图象上异于点 的一点,直线 交 轴于点 ,设直线 所对应的函数表达式为 .
①若 的面积为12,求 、 的值;
②作 轴,垂足为 ,记 ,求 的值.
