为了解某地区中学生一周课外阅读时长的情况，随机抽取部分中学生进行调查，根据调查结果，将阅读时长分为四类：2小时以内， 小时（含2小时）， 小时（含4小时），6小时及以上，并绘制了如图所示尚不完整的统计图．
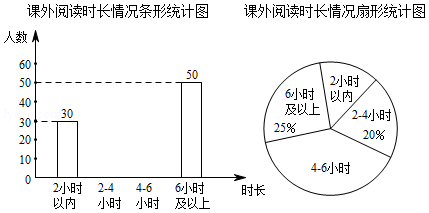
（1）本次调查共随机抽取了 名中学生，其中课外阅读时长“ 小时”的有 人；
（2）扇形统计图中，课外阅读时长“ 小时”对应的圆心角度数为 ；
（3）若该地区共有20000名中学生，估计该地区中学生一周课外阅读时长不少于4小时的人数．
如图，点B、C、D都在⊙O上，过点C作AC∥BD交OB延长线于点A，连接CD，且∠CDB=∠OBD=30°，B=6
cm． 
（1）求证：AC是⊙O的切线；
（2）求由弦CD、BD与弧BC所围成的阴影部分的面积．（结果保留π）
图1、图2是两张形状、大小完全相同的方格纸，方格纸中的每个小正方形的边长均为1，点A和点B在小正方形的顶点上．请你在图1、图2中各画出一个直角三角形，使所画两直角三角形的形状不同（另一顶点为小正方形的顶点）．
|+（
-1）0+cos45°．在平面直角坐标系xoy中， 一块含60°角的三角板作如图摆放，斜边AB在x轴上，直角顶点C在y轴正半轴上，已知点A（－1，0）．
（1）请直接写出点B、C的坐标：B（，）、C（，）；并求经过A、B、C三点的抛物线解析式；
（2）现有与上述三角板完全一样的三角板DEF（其中∠EDF=90°，∠DEF=60°），把顶点E放在线段AB上（点E是不与A、B两点重合的动点），并使ED所在直线经过点C．此时，EF所在直线与（1）中的抛物线交于第一象限的点M．
①设AE=x，当x为何值时，△OCE∽△OBC；
②在①被满足的情况下探究：抛物线的对称轴上是否存在点P使△PEM是等腰三角形，若存在，请求出点P的坐标；若不存在，请说明理由．
,AE＝3,求AF的长.
粤公网安备 44130202000953号