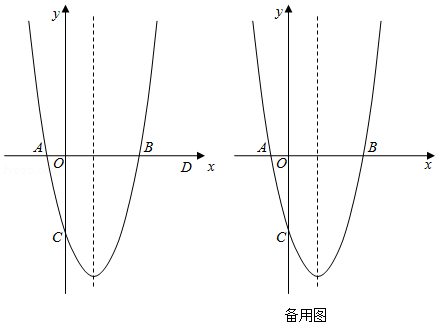
如图,抛物线 的对称轴为直线 ,抛物线与 轴交于点 和点 ,与 轴交于点 ,且点 的坐标为 .
(1)求抛物线的函数表达式;
(2)将抛物线 图象 轴下方部分沿 轴向上翻折,保留抛物线在 轴上的点和 轴上方图象,得到的新图象与直线 恒有四个交点,从左到右四个交点依次记为 , , , .当以 为直径的圆过点 时,求 的值;
(3)在抛物线 上,当 时, 的取值范围是 ,请直接写出 的取值范围.
推荐套卷
如图,抛物线 的对称轴为直线 ,抛物线与 轴交于点 和点 ,与 轴交于点 ,且点 的坐标为 .
(1)求抛物线的函数表达式;
(2)将抛物线 图象 轴下方部分沿 轴向上翻折,保留抛物线在 轴上的点和 轴上方图象,得到的新图象与直线 恒有四个交点,从左到右四个交点依次记为 , , , .当以 为直径的圆过点 时,求 的值;
(3)在抛物线 上,当 时, 的取值范围是 ,请直接写出 的取值范围.
