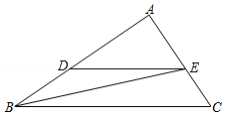
如图，在 中， ． ， ，若动点 从 出发，沿线段 运动到点 为止（不考虑 与 ， 重合的情况），运动速度为 ，过点 作 交 于点 ，连接 ，设动点 运动的时间为 ， 的长为 ．
（1）求 关于 的函数表达式，并写出自变量 的取值范围；
（2）当 为何值时， 的面积 有最大值？最大值为多少？
相关试题
某初级中学数学兴趣小组为了了解本校学生的年龄情况，随机调查了该校部分学生的年龄，整理数据并绘制如下不完整的统计图．
依据以上信息解答以下问题：
（1）求样本容量；
（2）直接写出样本的平均数，众数和中位数；
（3）若该校一共有1800名学生，估计该校年龄在15岁及以上的学生人数．
如图，抛物线 过点 ，对称轴是直线 ，且抛物线与 轴的正半轴交于点 ．
（1）求抛物线的解析式，并根据图象直接写出当 时，自变量 的取值范围；
（2）在第二象限内的抛物线上有一点 ，当 时，求 的面积．
相关知识点
推荐套卷
粤公网安备 44130202000953号