抛物线 与平行于 轴的直线交于 、 两点,且 点坐标为 ,请结合图象分析以下结论:①对称轴为直线 ;②抛物线与 轴交点坐标为 ;③ ;④若抛物线 与线段 恰有一个公共点,则 的取值范围是 ;⑤不等式 的解作为函数 的自变量的取值时,对应的函数值均为正数,其中正确结论的个数有
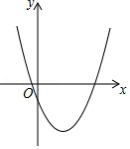
A.2个B.3个C.4个D.5个
推荐套卷
抛物线 与平行于 轴的直线交于 、 两点,且 点坐标为 ,请结合图象分析以下结论:①对称轴为直线 ;②抛物线与 轴交点坐标为 ;③ ;④若抛物线 与线段 恰有一个公共点,则 的取值范围是 ;⑤不等式 的解作为函数 的自变量的取值时,对应的函数值均为正数,其中正确结论的个数有

A.2个B.3个C.4个D.5个