阅读以下材料:
对数的创始人是苏格兰数学家纳皮尔
.
,
年),纳皮尔发明对数是在指数书写方式之前,直到18世纪瑞士数学家欧拉
,
年)才发现指数与对数之间的联系.
对数的定义:一般地,若
且
,那么
叫做以
为底
的对数,记作
,比如指数式
可以转化为对数式
,对数式
,可以转化为指数式
.
我们根据对数的定义可得到对数的一个性质:
,
,
,
,理由如下:
设
,
,则
,
,
,由对数的定义得
又
根据阅读材料,解决以下问题:
(1)将指数式
转化为对数式 ;
(2)求证:
,
,
,
(3)拓展运用:计算
.
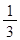 AC,求线段BD的长。
AC,求线段BD的长。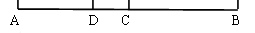
 的单项式
的单项式 与单项式
与单项式 是同类项,并且
是同类项,并且 ,当m 的倒数是-1,n的相反数是
,当m 的倒数是-1,n的相反数是 时,求
时,求 的值。
的值。 粤公网安备 44130202000953号
粤公网安备 44130202000953号