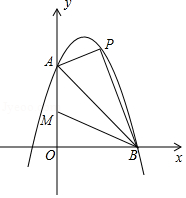
如图,已知抛物线 与 轴交于点 ,与 轴交于点 ,点 是线段 上方抛物线上的一个动点.
(1)求这条抛物线的表达式及其顶点坐标;
(2)当点 移动到抛物线的什么位置时,使得 ,求出此时点 的坐标;
(3)当点 从 点出发沿线段 上方的抛物线向终点 移动,在移动中,点 的横坐标以每秒1个单位长度的速度变动;与此同时点 以每秒1个单位长度的速度沿 向终点 移动,点 , 移动到各自终点时停止.当两个动点移动 秒时,求四边形 的面积 关于 的函数表达式,并求 为何值时, 有最大值,最大值是多少?
相关知识点
推荐套卷
 <
< +1(2)
+1(2)

 粤公网安备 44130202000953号
粤公网安备 44130202000953号