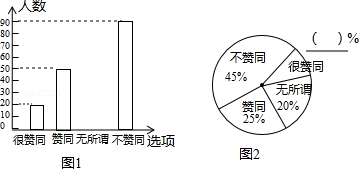
学校为了了解全校1600名学生对“初中学生带手机上学”现象的看法，在全校随机抽取了若干名学生进行问卷调查．问卷给出了四种看法供学生选择，每人只能选一种，且不能不选．将调查结果整理后，绘制成如图①、图②所示的条形统计图与扇形统计图（均不完整）．

（1）在这次调查中，一共抽取了多少名学生？

（2）补全条形统计图和扇形统计图；

（3）估计全校有多少名学生对“初中学生带手机上学”现象持“不赞同”的看法．