阅读理解:
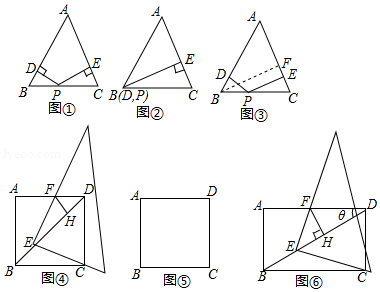
问题:我们在研究“等腰三角形底边上的任意一点到两腰的距离和为定值”时,如图①,在 中, ,点 为底边 上的任意一点, 于点 , 于点 ,求证: 是定值,在这个问题中,我们是如何找到这一定值的呢?
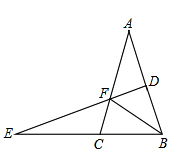
思路:我们可以将底边 上的任意一点 移动到特殊的位置,如图②,将点 移动到底边的端点 处,这样,点 、 都与点 重合,此时, , ,这样 .因此,在证明这一命题时,我们可以过点 作 边上的高 (如图③ ,证明 即可.
请利用上述探索定值问题的思路,解决下列问题:
如图④,在正方形 中,一直角三角板的直角顶点 在对角线 上运动,一条直角边始终经过点 ,另一条直角边与射线 相交于点 ,过点 作 ,垂足为 .
(1)试猜想 与 的数量关系,并加以证明;
(2)当点 在 的延长线上运动时, 与 之间存在怎样的数量关系?请在图⑤中画出图形并直接写出结论;
(3)如图⑥所示,如果将正方形 改为矩形 , ,其它条件不变,请直接写出 与 的数量关系.
相关知识点
推荐套卷
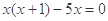 ②
②
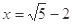 ,求
,求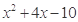 的值
的值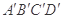 与四边形ABCD关于O点中心对称
与四边形ABCD关于O点中心对称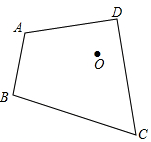

 粤公网安备 44130202000953号
粤公网安备 44130202000953号