（探究证明）
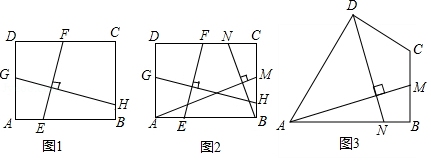
（1）某班数学课题学习小组对矩形内两条互相垂直的线段与矩形两邻边的数量关系进行探究，提出下列问题，请你给出证明．
如图1，矩形 中， ， 分别交 ， 于点 ， ， 分别交 ， 于点 ， ．求证： ；
（结论应用）
（2）如图2，在满足（1）的条件下，又 ，点 ， 分别在边 ， 上，若 ，则 的值为 ；
（联系拓展）
（3）如图3，四边形 中， ， ， ， ，点 ， 分别在边 ， 上，求 的值．
已知：⊙O是△ABC的外接圆，点M为⊙O上一点.
（1）如图，若△ABC为等边三角形，BM=1，CM=2，求AM的长；
小明在解决这个问题时采用的方法是：延长MC到E，使ME=AM，从而可证△AME为等边三角形，并且△ABM≌△ACE，进而就可求出线段AM的长．
请你借鉴小明的方法写出AM的长，并写出推理过程．
（2）若△ABC为等腰直角三角形，∠BAC=
，
，
（其中
），直接写出AM的长(用含有a，b的代数式表示).
阅读下面的材料：
小明在学习中遇到这样一个问题：若1≤x≤m，求二次函数
的最大值．他画图研究后发现，
和
时的函数值相等，于是他认为需要对
进行分类讨论．他的解答过程如下：
∵二次函数的对称轴为直线
，
∴由对称性可知，和时的函数值相等．
∴若1≤m＜5，则时，
的最大值为2；
若m≥5，则
时，的最大值为
．
请你参考小明的思路，解答下列问题：
（1）当
≤x≤4时，二次函数
的最大值为_______；
（2）若p≤x≤2，求二次函数的最大值；
（3）若t≤x≤t+2时，二次函数的最大值为31，则
的值为_______．
）. 
某水果批发商销售每箱进价为40元的苹果，物价部门规定每箱售价不得高于55元，市场调查发现，若以每箱50元价格出售，平均每天销售90箱，价格每提高1元，平均每天少销售3箱.
（1）求平均每天销售量y（箱）与销售价x（元/箱）之间的函数关系式；
（2）求该批发商平均每天的销售利润w（元）与销售价x（元/箱）之间的函数关系式；
（3）当每箱苹果的销售价为多少元时，可以获得最大利润？
粤公网安备 44130202000953号