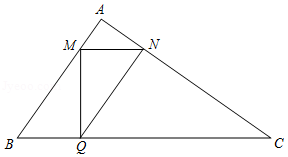
如图,在 中, , , ,点 , 分别是边 , 上的动点(点 不与 , 重合),且 ,过点 作 的平行线 ,交 于点 ,连接 ,设 为 .
(1)试说明不论 为何值时,总有 ;
(2)是否存在一点 ,使得四边形 为平行四边形,试说明理由;
(3)当 为何值时,四边形 的面积最大,并求出最大值.
相关知识点
推荐套卷
如图,在 中, , , ,点 , 分别是边 , 上的动点(点 不与 , 重合),且 ,过点 作 的平行线 ,交 于点 ,连接 ,设 为 .
(1)试说明不论 为何值时,总有 ;
(2)是否存在一点 ,使得四边形 为平行四边形,试说明理由;
(3)当 为何值时,四边形 的面积最大,并求出最大值.
