某工厂计划生产一种创新产品，若生产一件这种产品需 种原料1.2千克、 种原料1千克．已知 种原料每千克的价格比 种原料每千克的价格多10元．
（1）为使每件产品的成本价不超过34元，那么购入的 种原料每千克的价格最高不超过多少元？
（2）将这种产品投放市场批发销售一段时间后，为拓展销路又开展了零售业务，每件产品的零售价比批发价多30元．现用10000元通过批发价购买该产品的件数与用16000元通过零售价购买该产品的件数相同，那么这种产品的批发价是多少元？
相关试题
用心做一做、细心算一算（每小题5分 ，共25分 ）
(1)、－24－（10－15） (2)、0－
÷[
－(－4)]
(3)、－24×(
) (4)、－×2－3×
(5)、[(-3)2-(-5)2]÷(-2)
；
.
；（2）
，且两条直角边的长b和c恰好是这个方程的两个根时，求k的值．相关知识点
推荐套卷
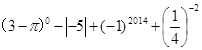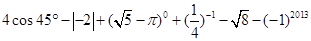
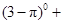
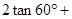
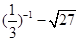粤公网安备 44130202000953号