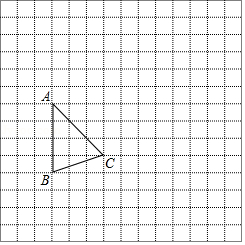
如图，在网格中，每个小正方形的边长均为1个单位长度．我们将小

首页 / 初中数学 / 试题详细

更新 2022-09-04
科目数学
题型解答题
难度中等
浏览 178

挑错有奖

如图，在网格中，每个小正方形的边长均为1个单位长度．我们将小正方形的顶点叫做格点， $ΔABC$ 的三个顶点均在格点上．

（1）将 $ΔABC$ 先向右平移6个单位长度，再向上平移3个单位长度，得到△ $A_{1} B_{1} C_{1}$ ，画出平移后的△ $A_{1} B_{1} C_{1}$ ；

（2）建立适当的平面直角坐标系，使得点 $A$ 的坐标为 $(- 4, 3)$ ；

（3）在（2）的条件下，直接写出点 $A_{1}$ 的坐标．

登录免费查看答案和解析

相关试题

下列8个事件中：
（1）掷一枚硬币，正面朝上。
（2）打开电视机，正在播电视剧。
（3）随意翻开一本有400页的书，正好翻到第200页。
（4）天上下雨，马路潮湿。
（5）你能长到身高5米。
（6）买奖券中特等大奖。
（7）掷一枚骰子的得到的点数小于8。
（8）2005年6月27日是星期一。
其中（将序号填入题中的横线上即可）
不可能事件为　　　　　　　　　；必然事件为　　　　　　　　　；
不确定事件中，发生可能性最大的是　　　　，发生可能性最小的是　　　　　