如图,已知抛物线 经过点 、 和 , 垂直于 轴,交抛物线于点 , 垂直于 轴,垂足为 ,直线 是该抛物线的对称轴,点 是抛物线的顶点.
(1)求出该二次函数的表达式及点 的坐标;
(2)若 沿 轴向右平移,使其直角边 与对称轴 重合,再沿对称轴 向上平移到点 与点 重合,得到 △ ,求此时 △ 与矩形 重叠部分图形的面积;
(3)若 沿 轴向右平移 个单位长度 得到 △ , △ 与 重叠部分图形的面积记为 ,求 与 之间的函数表达式,并写出自变量 的取值范围.

相关知识点
推荐套卷
 。已知算式
。已知算式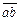 ´0.c5d=
´0.c5d= 中a,b,c,d,e,f都是
中a,b,c,d,e,f都是 的所有的非0自然数整除,我们称自然数n为“牛数”。
的所有的非0自然数整除,我们称自然数n为“牛数”。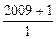 ],[
],[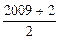 ],[
],[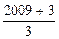 ],…,[
],…,[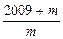 ]。
]。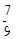 时。现在,甲和乙都最多只能工作60小时,丙最多只能工作35小时,三队工作时间之和为100小时完成工程,则甲最多工作多少小时?
时。现在,甲和乙都最多只能工作60小时,丙最多只能工作35小时,三队工作时间之和为100小时完成工程,则甲最多工作多少小时? 粤公网安备 44130202000953号
粤公网安备 44130202000953号