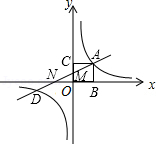
如图,正方形 的面积为4,反比例函数 的图象经过点 ,过点 的直线 与 的图象相交于第三象限的点 ,且点 到 轴的距离为4.
(1)求反比例函数 和一次函数 的解析式.
(2)当 时,观察函数 的图象,直接写出 的取值范围.
(3)直线 与坐标轴交于 、 两点,求 外接圆的面积.
推荐套卷
如图,正方形 的面积为4,反比例函数 的图象经过点 ,过点 的直线 与 的图象相交于第三象限的点 ,且点 到 轴的距离为4.
(1)求反比例函数 和一次函数 的解析式.
(2)当 时,观察函数 的图象,直接写出 的取值范围.
(3)直线 与坐标轴交于 、 两点,求 外接圆的面积.
