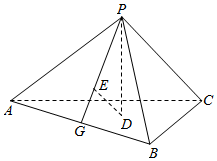
如图,已知正三棱锥 的侧面是直角三角形, ,顶点P在平面ABC内的正投影为点D,D在平面PAB内的正投影为点E,连接PE并延长交AB于点G.
(Ⅰ)证明:G是AB的中点;
(Ⅱ)在图中作出点E在平面PAC内的正投影F(说明作法及理由),并求四面体PDEF的体积.
推荐套卷
如图,已知正三棱锥 的侧面是直角三角形, ,顶点P在平面ABC内的正投影为点D,D在平面PAB内的正投影为点E,连接PE并延长交AB于点G.
(Ⅰ)证明:G是AB的中点;
(Ⅱ)在图中作出点E在平面PAC内的正投影F(说明作法及理由),并求四面体PDEF的体积.
