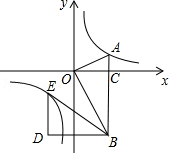
如图,在平面直角坐标系中,OA⊥OB,AB⊥x轴于点C,点A( ,1)在反比例函数 的图象上.
(1)求反比例函数 的表达式;
(2)在x轴的负半轴上存在一点P,使得S△AOP= S△AOB,求点P的坐标;
(3)若将△BOA绕点B按逆时针方向旋转60°得到△BDE.直接写出点E的坐标,并判断点E是否在该反比例函数的图象上,说明理由.
推荐套卷
如图,在平面直角坐标系中,OA⊥OB,AB⊥x轴于点C,点A( ,1)在反比例函数 的图象上.
(1)求反比例函数 的表达式;
(2)在x轴的负半轴上存在一点P,使得S△AOP= S△AOB,求点P的坐标;
(3)若将△BOA绕点B按逆时针方向旋转60°得到△BDE.直接写出点E的坐标,并判断点E是否在该反比例函数的图象上,说明理由.
