小李是某服装厂的一名工人,负责加工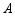 ,
,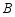 两种型号服装,他每月的工作时间为22天,月收入由底薪和计件工资两部分组成,其中底薪900元,加工
两种型号服装,他每月的工作时间为22天,月收入由底薪和计件工资两部分组成,其中底薪900元,加工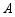 型服装1件可得20元,加工
型服装1件可得20元,加工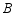 型服装1件可得12元.已知小李每天可加工
型服装1件可得12元.已知小李每天可加工 型服装4件或
型服装4件或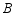 型服装8件,设他每月加工
型服装8件,设他每月加工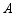 型服装的时间为
型服装的时间为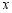 天,月收入为
天,月收入为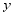 元.
元.
(1)求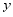 与
与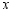 的函数关系式;
的函数关系式;
(2)根据服装厂要求,小李每月加工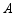 型服装数量应不少于
型服装数量应不少于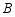 型服装数量的
,那么他的月收入最高能达到多少元?
型服装数量的
,那么他的月收入最高能达到多少元?
相关知识点
推荐套卷
小李是某服装厂的一名工人,负责加工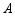 ,
,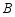 两种型号服装,他每月的工作时间为22天,月收入由底薪和计件工资两部分组成,其中底薪900元,加工
两种型号服装,他每月的工作时间为22天,月收入由底薪和计件工资两部分组成,其中底薪900元,加工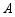 型服装1件可得20元,加工
型服装1件可得20元,加工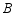 型服装1件可得12元.已知小李每天可加工
型服装1件可得12元.已知小李每天可加工 型服装4件或
型服装4件或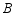 型服装8件,设他每月加工
型服装8件,设他每月加工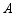 型服装的时间为
型服装的时间为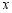 天,月收入为
天,月收入为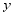 元.
元.
(1)求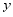 与
与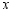 的函数关系式;
的函数关系式;
(2)根据服装厂要求,小李每月加工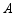 型服装数量应不少于
型服装数量应不少于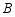 型服装数量的
,那么他的月收入最高能达到多少元?
型服装数量的
,那么他的月收入最高能达到多少元?