如图所示,二次函数的图象(记为抛物线与轴交于点,与轴分别交于点、,点、的横坐标分别记为,,且.
(1)若,,且过点,求该二次函数的表达式;
(2)若关于的一元二次方程的判别式△.求证:当时,二次函数的图象与轴没有交点.
(3)若,点的坐标为,,过点作直线垂直于轴,且抛物线的的顶点在直线上,连接、、,的延长线与抛物线交于点,若,求的最小值.
推荐套卷
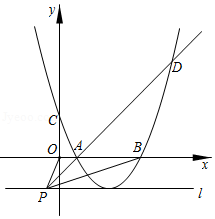
如图所示,二次函数的图象(记为抛物线与轴交于点,与轴分别交于点、,点、的横坐标分别记为,,且.
(1)若,,且过点,求该二次函数的表达式;
(2)若关于的一元二次方程的判别式△.求证:当时,二次函数的图象与轴没有交点.
(3)若,点的坐标为,,过点作直线垂直于轴,且抛物线的的顶点在直线上,连接、、,的延长线与抛物线交于点,若,求的最小值.
