在平面直角坐标系中,已知抛物线 与 轴交于 , 两点(点 在点 的左侧),与 轴交于点 ,顶点为点 .
(1)当 时,直接写出点 , , , 的坐标:
, , , ;
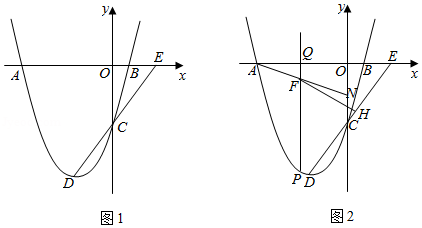
(2)如图1,直线 交 轴于点 ,若 ,求 的值和 的长;
(3)如图2,在(2)的条件下,若点 为 的中点,动点 在第三象限的抛物线上,过点 作 轴的垂线,垂足为 ,交 于点 ;过点 作 ,垂足为 .设点 的横坐标为 ,记 .
①用含 的代数式表示 ;
②设 ,求 的最大值.
相关知识点
推荐套卷

 ∠BOC,∠COD=∠AOD=3∠AOB,求∠AOB和∠COD的度数。
∠BOC,∠COD=∠AOD=3∠AOB,求∠AOB和∠COD的度数。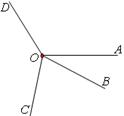
 AC,D、E分别为AC、AB的中点,求DE的长。
AC,D、E分别为AC、AB的中点,求DE的长。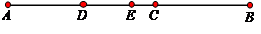

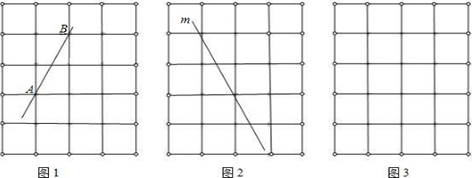
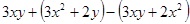 ,其中
,其中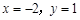 ;
;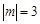 ,求
,求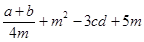 的值。
的值。 粤公网安备 44130202000953号
粤公网安备 44130202000953号