“今有善行者行一百步,不善行者行六十步.”(出自《九章算术》意思是:同样时间段内,走路快的人能走100步,走路慢的人只能走60步.假定两者步长相等,据此回答以下问题:
(1)今不善行者先行一百步,善行者追之,不善行者再行六百步,问孰至于前,两者几何步隔之?即:走路慢的人先走100步,走路快的人开始追赶,当走路慢的人再走600步时,请问谁在前面,两人相隔多少步?
(2)今不善行者先行两百步,善行者追之,问几何步及之?即:走路慢的人先走200步,请问走路快的人走多少步才能追上走路慢的人?
相关知识点
推荐套卷
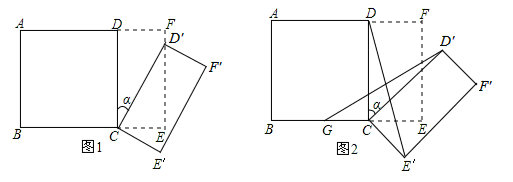
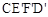 ,旋转角为
,旋转角为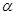 .
.
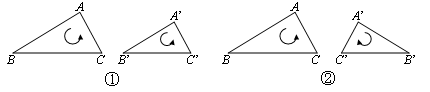
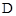 恰好落在EF边上时,求旋转角
恰好落在EF边上时,求旋转角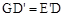 ;
; 与
与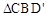 能否全等?若能,直接写出旋转角
能否全等?若能,直接写出旋转角 ,比如:
,比如: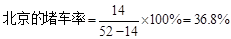 ;
;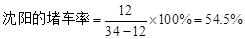 .某人欲从北京、沈阳、上海、温州四个城市中任意选取两个作为出发目的地,求选取的两个城市的堵车率都超过30%的概率.
.某人欲从北京、沈阳、上海、温州四个城市中任意选取两个作为出发目的地,求选取的两个城市的堵车率都超过30%的概率.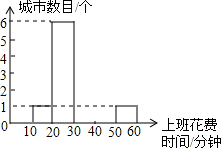


 粤公网安备 44130202000953号
粤公网安备 44130202000953号