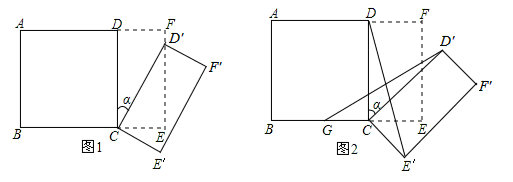
如图1所示，将一个边长为2的正方形ABCD和一个长为2、宽为1的长方形CEFD拼在一起，构成一个大的长方形ABEF.现将小长方形CEFD绕点C顺时针旋转至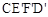
,旋转角为
.
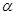（1）当点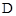
恰好落在EF边上时，求旋转角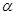的值；
（2）如图2，G为BC的中点，且00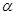＜＜900，求证：
；
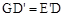（3）小长方形CEFD绕点C顺时针旋转一周的过程中，
与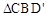
能否全等？若能，直接写出旋转角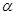的值；若不能，说明理由.
推荐套卷
如图1所示，将一个边长为2的正方形ABCD和一个长为2、宽为1的长方形CEFD拼在一起，构成一个大的长方形ABEF.现将小长方形CEFD绕点C顺时针旋转至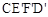,旋转角为.
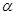（1）当点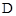恰好落在EF边上时，求旋转角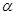的值；
（2）如图2，G为BC的中点，且00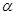＜＜900，求证：；
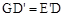（3）小长方形CEFD绕点C顺时针旋转一周的过程中，与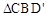能否全等？若能，直接写出旋转角的值；若不能，说明理由.
粤公网安备 44130202000953号