公元前5世纪,毕达哥拉斯学派中的一名成员希伯索斯发现了无理数 ,导致了第一次数学危机, 是无理数的证明如下:
假设 是有理数,那么它可以表示成 与 是互质的两个正整数).于是 ,所以, .于是 是偶数,进而 是偶数,从而可设 ,所以 , ,于是可得 也是偶数.这与" 与 是互质的两个正整数"矛盾.从而可知" 是有理数"的假设不成立,所以, 是无理数.
这种证明" 是无理数"的方法是
| A. |
综合法 |
B. |
反证法 |
C. |
举反例法 |
D. |
数学归纳法 |
相关知识点
推荐套卷


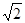 和5.1,则A、B两点之间表示整数的点共有( )
和5.1,则A、B两点之间表示整数的点共有( )
 粤公网安备 44130202000953号
粤公网安备 44130202000953号