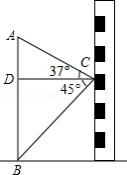
如图,小东在教学楼距地面9米高的窗口 处,测得正前方旗杆顶部 点的仰角为 ,旗杆底部 点的俯角为 ,升旗时,国旗上端悬挂在距地面2.25米处,若国旗随国歌声冉冉升起,并在国歌播放45秒结束时到达旗杆顶端,则国旗应以多少米 秒的速度匀速上升?(参考数据: , ,
相关知识点
推荐套卷
如图,小东在教学楼距地面9米高的窗口 处,测得正前方旗杆顶部 点的仰角为 ,旗杆底部 点的俯角为 ,升旗时,国旗上端悬挂在距地面2.25米处,若国旗随国歌声冉冉升起,并在国歌播放45秒结束时到达旗杆顶端,则国旗应以多少米 秒的速度匀速上升?(参考数据: , ,
