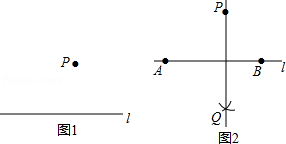下面是"经过已知直线外一点作这条直线的垂线"的尺规作图过程：
已知：直线 和 外一点 ．（如图
求作：直线 的垂线，使它经过点 ．
作法：如图2
（1）在直线 上任取两点 ， ；
（2）分别以点 ， 为圆心， ， 长为半径作弧，两弧相交于点 ；
（3）作直线 ．
所以直线 就是所求的垂线．
请回答：该作图的依据是 ．
=0，则x+2y=__________.
的相反数为_______；倒数为________；
。
；
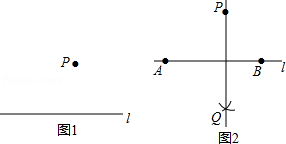
相关知识点
推荐套卷
下面是"经过已知直线外一点作这条直线的垂线"的尺规作图过程：
已知：直线 和 外一点 ．（如图
求作：直线 的垂线，使它经过点 ．
作法：如图2
（1）在直线 上任取两点 ， ；
（2）分别以点 ， 为圆心， ， 长为半径作弧，两弧相交于点 ；
（3）作直线 ．
所以直线 就是所求的垂线．
请回答：该作图的依据是 ．
粤公网安备 44130202000953号