如图,直线y=k(x-2)+k-1与x轴、y轴分别交于B、C两点,且 .
.
(1)求B点坐标和k值;
(2)若点A(x,y)是直线y=k(x-2)+k-1(k>0)上在第一象限内的一个动点,
①当点A在运动过程中,试写出△AOB的面积S与x的函数关系式;(不要求写出自变量的取值范围)
②当A点运动到什么位置时,△AOB的面积为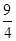 ,并说明理由;
,并说明理由;
③在②成立的情况下,x轴上是否存在一点P,使△AOP是等腰三角形?若存在,请直接写出满足条件的所有P点坐标;若不存在,请说明理由.
相关知识点
推荐套卷
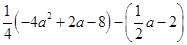 ,其中
,其中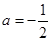 .
.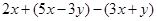
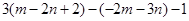 .
.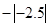 ,
,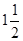 ,
,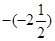 ,
,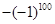 ,
,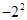 .
.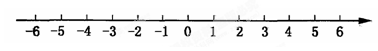

 粤公网安备 44130202000953号
粤公网安备 44130202000953号