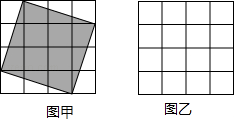
如图,在甲、乙两个4×4的方格图中,每个小正方形的边长都为1.
(1)请求出图甲中阴影正方形的面积和边长;
(2)请在图乙中画一个与图甲阴影部分面积不相等的正方形,要求它的边长为无理数,并求出它的边长.
注:答案直接写在图下方的横线上即可.
甲:面积= ;边长= .
乙:边长= .
相关知识点
推荐套卷
如图,在甲、乙两个4×4的方格图中,每个小正方形的边长都为1.
(1)请求出图甲中阴影正方形的面积和边长;
(2)请在图乙中画一个与图甲阴影部分面积不相等的正方形,要求它的边长为无理数,并求出它的边长.
注:答案直接写在图下方的横线上即可.
甲:面积= ;边长= .
乙:边长= .
