如图,A、B表示两个村庄,直线X表示高速公路,已知AB=50km,A、B到直线X的距离分别为10km和40km,要在高速公路旁修建一出口P.小民设计了两种方案,图(1)是方案一的示意图(AP与直线X垂直,垂足为P),P到A、B的距离之和S1=PA+PB; 图(2)是方案二的示意图(点A关于直线X的对称点是A',连接BA'交直线X于点P),P到A、B的距离之和S2=PA+PB.
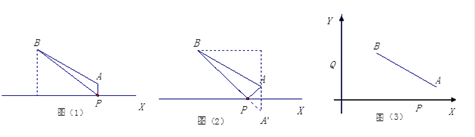
(1)求S1 、S2 ,并比较它们的大小.
(2)请你说明S2=PA+PB的值为最小.
(3)拟建的另一高速公路Y与高速公路X垂直,建立如图所示的直角坐标系,B到直线Y的距离为30km,请你在X旁和Y旁各修建一出口P、Q,使P、A、B、Q 组成的四边形的周长最小.并求出这个最小值.