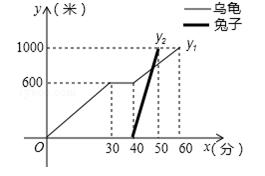
“龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场.图中的函数图象刻画了“龟兔再次赛跑”的故事(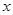 表示乌龟从起点出发所行的时间,
表示乌龟从起点出发所行的时间, 表示乌龟所行的路程,
表示乌龟所行的路程, 表示兔子所行的路程).有下列说法:
表示兔子所行的路程).有下列说法:
①“龟兔再次赛跑”的路程为1000米;
②兔子和乌龟同时从起点出发;
③乌龟在途中休息了10分钟;
④兔子在途中750米处追上乌龟.
其中正确的说法是 .(把你认为正确说法的序号都填上)
相关知识点
推荐套卷
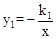 上,B、D在双曲线
上,B、D在双曲线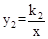 上,k1=2k2(k1>0),AB∥y轴,S△ABCD=24,则k1= .
上,k1=2k2(k1>0),AB∥y轴,S△ABCD=24,则k1= .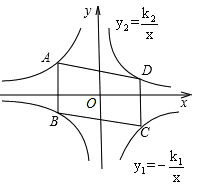
 粤公网安备 44130202000953号
粤公网安备 44130202000953号