如图，△ABC的边BC在直线l上，AD是△ABC的高，∠ABC=45°，BC=6cm，AB=2
cm．点P从点B出发沿BC方向以1cm/s速度向点C运动，当点P到点C时，停止运动．PQ⊥BC，PQ交AB或AC于点Q，以PQ为一边向右侧作矩形PQRS，PS=2PQ．矩形PQRS与△ABC的重叠部分的面积为S（cm2），点P的运动时间为t（s）．回答下列问题：
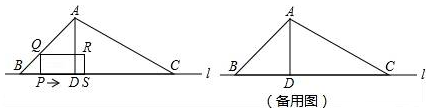
（1）AD= cm；
（2）当点R在边AC上时，求t的值；
（3）求S与t之间的函数关系式．
相关试题
有20筐白菜，以每筐25千克为标准，超过或不足的分别用正、负来表示，记录如下：
| 与标准质量的差（单位：千克） |
－3 |
－2 |
－1.5 |
0 |
1 |
2.5 |
| 筐数 |
1 |
4 |
2 |
3 |
2 |
8 |
（1）与标准质量比较，20筐白菜总计超过或不足多少千克？
（2）若白菜每千克售价2.6元，则出售这20筐白菜可卖多少元？
，求代数式
的值.
，|-2.5|，0，-22，-（+2），表示在数轴上，并用“<”将它们连接起来.
，
，
，
，
，
，
按要求分别填入相应的集合中.相关知识点
推荐套卷
粤公网安备 44130202000953号