如图1是一个长为2a、宽为2b的长方形(其中a,b均为正数,且a>b),沿图中虚线用剪刀均匀分成四块相同小长方形,然后按图2方式拼成一个大正方形.
(1)你认为图2中大正方形的边长为a+b ;小正方形(阴影部分)的边长为 .(用含a、b的代数式表示)
(2)仔细观察图2,请你写出下列三个代数式:(a+b)2,(a-b)2,ab所表示的图形面积之间的相等关系,并选取适合a、b的数值加以验证.
(3)已知a+b=7,ab=6.求代数式(a-b)的值.

相关知识点
推荐套卷
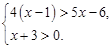
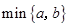 的含义为:当
的含义为:当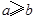 时,
时, 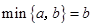 ;当
;当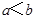 时,
时, 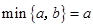 .如:
.如: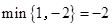 ,
,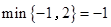 .
.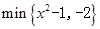 ;
;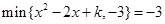 , 求实数
, 求实数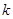 的取值范围;
的取值范围;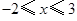 时,
时,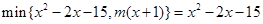 .直接写出实数
.直接写出实数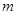 的取值范围.
的取值范围.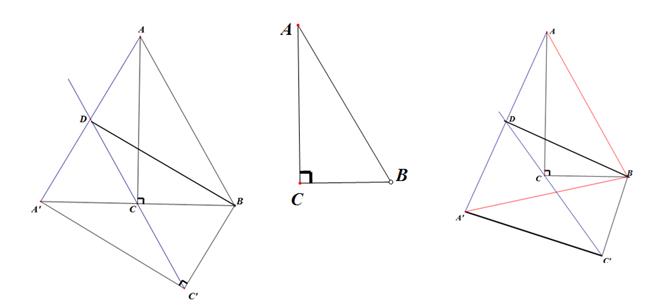
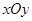 中,抛物线
中,抛物线 过点
过点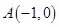 ,
,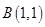 ,与
,与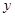 轴交于点
轴交于点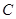 .
.
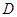 在抛物线
在抛物线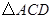 的周长最小时,求点
的周长最小时,求点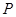 ,使
,使 成为以
成为以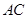 为直角边的直角三角形?若存在,求出点
为直角边的直角三角形?若存在,求出点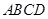 中,对角线
中,对角线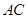 与
与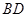 交于点
交于点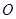 ,
,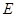 是
是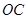 上任意一点,
上任意一点,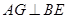 于点
于点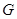 ,交
,交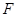 .
.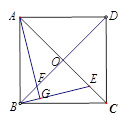

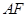 与
与 的数量关系;
的数量关系;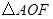 和
和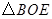 中,可以通过证明
中,可以通过证明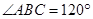 ,请参考明明思考问题的方法,求
,请参考明明思考问题的方法,求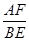 的值.
的值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号