某校的一间阶梯教室,第1排的座位数为12,从第2排开始,每一排都比前一排增加a个座位.
(1)请你在下表的空格里填写一个适当的代数式:
| 排数 |
第1排 |
第2排 |
第3排 |
第4排 |
… |
第n排 |
| 座位数 |
12 |
12+a |
|
|
… |
|
已知第15排座位数是第5排座位数的2倍,求a的值,并计算第21排有多少个座位?
相关知识点
推荐套卷


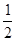 。这样,前一批同学每人比原来少分摊1.5元车费,求参加旅游的同学共有多少人?
。这样,前一批同学每人比原来少分摊1.5元车费,求参加旅游的同学共有多少人? 粤公网安备 44130202000953号
粤公网安备 44130202000953号