一盒中装有9张各写有一个数字的卡片，其中4张卡片上的数字是1，3张卡片上的数字是2，2张卡片上的数字是3，从盒中任取3张卡片．
（1）求所取3张卡片上的数字完全相同的概率；
（2）
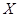表示所取3张卡片上的数字的中位数，求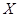的分布列与数学期望．
（注：若三个数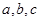
满足 
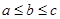，则称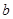
为这三个数的中位数）．
相关试题
上的不同三点，O是
满足
，记
；
}的前n项和为
，已知对任意的
，点
，均在函数
且
均为常数)的图像上.
求数列
的前
项和
.
，且
.
表示为
的函数
，并求
分别为
的三个内角
对应的边长，若
，求
的最大值为
．
，求t的取值范围，并把f(x)表示为t的函数m(t) ；
的所有实数a．推荐套卷
一盒中装有9张各写有一个数字的卡片，其中4张卡片上的数字是1，3张卡片上的数字是2，2张卡片上的数字是3，从盒中任取3张卡片．
（1）求所取3张卡片上的数字完全相同的概率；
（2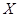）表示所取3张卡片上的数字的中位数，求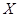的分布列与数学期望．
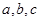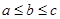（注：若三个数满足 ，则称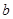为这三个数的中位数）．
粤公网安备 44130202000953号