已知椭圆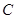 :
: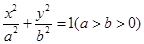 ,右焦点
,右焦点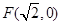 ,点
,点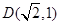 在椭圆上.
在椭圆上.
(Ⅰ)求椭圆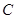 的标准方程;
的标准方程;
(Ⅱ)已知直线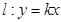 与椭圆
与椭圆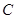 交于
交于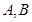 两点,
两点,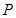 为椭圆
为椭圆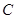 上异于
上异于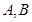 的动点.
的动点.
(1)若直线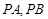 的斜率都存在,证明:
的斜率都存在,证明: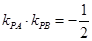 ;
;
(2)若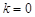 ,直线
,直线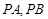 分别与直线
分别与直线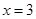 相交于点
相交于点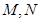 ,直线
,直线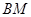 与椭圆
与椭圆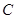 相交于点
相交于点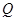 (异于点
(异于点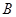 ), 求证:
), 求证: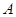 ,
,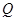 ,
,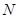 三点共线.
三点共线.
推荐套卷
已知椭圆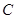 :
: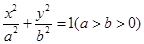 ,右焦点
,右焦点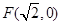 ,点
,点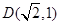 在椭圆上.
在椭圆上.
(Ⅰ)求椭圆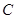 的标准方程;
的标准方程;
(Ⅱ)已知直线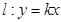 与椭圆
与椭圆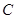 交于
交于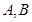 两点,
两点,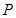 为椭圆
为椭圆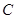 上异于
上异于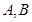 的动点.
的动点.
(1)若直线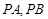 的斜率都存在,证明:
的斜率都存在,证明: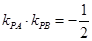 ;
;
(2)若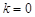 ,直线
,直线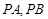 分别与直线
分别与直线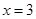 相交于点
相交于点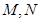 ,直线
,直线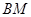 与椭圆
与椭圆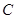 相交于点
相交于点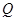 (异于点
(异于点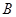 ), 求证:
), 求证: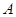 ,
,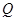 ,
,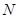 三点共线.
三点共线.