某车间
名工人年龄数据如下表：
| 年龄（岁） |
工人数（人） |
 |
 |
 |
 |
 |
|
 |
 |
 |
 |
 |
|
 |
|
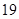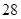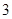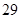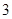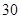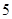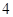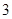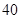| 合计 |
|
（1）求这名工人年龄的众数与极差；
（2）以十位数为茎，个位数为叶，作出这名工人年龄的茎叶图；
（3）求这名工人年龄的方差．
的不等式
，
的解集分别为
，
，且
，问这样的
存在吗？若存在，求出
，
，求
的值．
，
，求
的值．
，集合
，求
．
是周期为
的周期函数吗？为什么？判断函数
是否为周期函数？推荐套卷
某车间名工人年龄数据如下表：
| 年龄（岁） |
工人数（人） |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
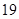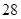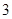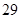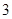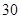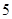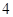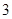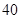| 合计 |
|
（1）求这名工人年龄的众数与极差；
（2）以十位数为茎，个位数为叶，作出这名工人年龄的茎叶图；
（3）求这名工人年龄的方差．
粤公网安备 44130202000953号