如图，已知AF
平面ABCD，四边形ABEF为矩形，四边形ABCD为直角梯形，
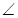DAB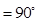
，AB//CD，AD
AFCD2，AB4． 
（Ⅰ）求证：AC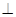
平面BCE；
（Ⅱ）求三棱锥A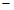
CDE的体积；
（Ⅲ）线段EF上是否存在一点M，使得BMCE ?若存在，确定M点的位置；若不存在，请说明理由．
与直线y=x+2
与复数
的共轭复数相等，求x，y.
与抛物线
所围成的图形面积是推荐套卷
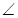如图，已知AF平面ABCD，四边形ABEF为矩形，四边形ABCD为直角梯形，DAB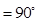，AB//CD，ADAFCD2，AB4．
（Ⅰ）求证：AC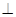平面BCE；
（Ⅱ）求三棱锥A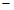CDE的体积；
（Ⅲ）线段EF上是否存在一点M，使得BMCE ?若存在，确定M点的位置；若不存在，请说明理由．
粤公网安备 44130202000953号