如图,矩形ABCD中,AB=8,AD=10.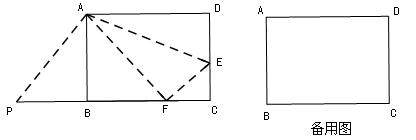
(1)求矩形ABCD的周长;
(2)E是CD上的点,将△ADE沿折痕AE折叠,使点D落在BC边上点F处.
①求DE的长;
② 点P是线段CB延长线上的点,连接PA,若△PAF是等腰三角形,求PB的长.
(3)M是AD上的动点,在DC 上存在点N,使△MDN沿折痕MN折叠,点D落在BC边上点T处,求线段CT长度的最大值与最小值之和.
推荐套卷
如图,矩形ABCD中,AB=8,AD=10.
(1)求矩形ABCD的周长;
(2)E是CD上的点,将△ADE沿折痕AE折叠,使点D落在BC边上点F处.
①求DE的长;
② 点P是线段CB延长线上的点,连接PA,若△PAF是等腰三角形,求PB的长.
(3)M是AD上的动点,在DC 上存在点N,使△MDN沿折痕MN折叠,点D落在BC边上点T处,求线段CT长度的最大值与最小值之和.