如图，已知椭圆C：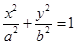
（a＞b＞0）的右焦点为F（c，0），下顶点为A（0，﹣b），直线AF与椭圆的右准线交于点B，若F恰好为线段AB的中点．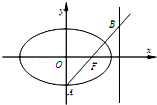
（1）求椭圆C的离心率；
（2）若直线AB与圆x2+y2=2相切，求椭圆C的方程．
相关试题
的底面为直角梯形，
，
,
底面
，且
，
是
的中点.
平面
；
与平面
，求二面角
的大小.
中，角
所对的边分别为
.已知
.
的值；
,其中
．．
满足什么条件时,
取得极值？
，且
上单调递增，试用
表示出
的取值范围．
.推荐套卷
如图，已知椭圆C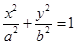：（a＞b＞0）的右焦点为F（c，0），下顶点为A（0，﹣b），直线AF与椭圆的右准线交于点B，若F恰好为线段AB的中点．
（1）求椭圆C的离心率；
（2）若直线AB与圆x2+y2=2相切，求椭圆C的方程．
粤公网安备 44130202000953号