某体育馆拟用运动场的边角地建一个矩形的健身室(如图所示),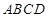 是一个标出为
是一个标出为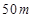 的正方形地皮,扇形
的正方形地皮,扇形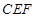 是运动场的一部分,其半径为
是运动场的一部分,其半径为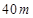 ,矩形
,矩形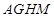 就是拟建的健身室,其中
就是拟建的健身室,其中 分别在
分别在 和
和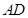 上,
上,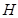 在
在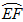 上,设矩形
上,设矩形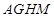 的面积为
的面积为 ,
, .
.
(I)请将 表示为
表示为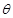 的函数,并指出当点
的函数,并指出当点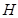 在
在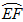 的何处时,该健身室的面积最大,最大面积是多少?
的何处时,该健身室的面积最大,最大面积是多少?
(II)由上面函数建立的思想,试求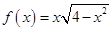 的最大值.
的最大值.
推荐套卷
某体育馆拟用运动场的边角地建一个矩形的健身室(如图所示),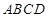 是一个标出为
是一个标出为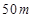 的正方形地皮,扇形
的正方形地皮,扇形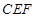 是运动场的一部分,其半径为
是运动场的一部分,其半径为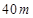 ,矩形
,矩形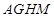 就是拟建的健身室,其中
就是拟建的健身室,其中 分别在
分别在 和
和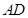 上,
上,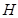 在
在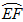 上,设矩形
上,设矩形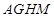 的面积为
的面积为 ,
, .
.
(I)请将 表示为
表示为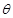 的函数,并指出当点
的函数,并指出当点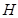 在
在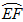 的何处时,该健身室的面积最大,最大面积是多少?
的何处时,该健身室的面积最大,最大面积是多少?
(II)由上面函数建立的思想,试求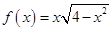 的最大值.
的最大值.