(本小题满分14分)
如图,P-ABC是底面边长为1的正三棱锥,D、E、F分别为棱长PA、PB、PC上的点, 截面DEF∥底面ABC, 且棱台DEF-ABC与棱锥P-ABC的棱长和相等.(棱长和是指多面体中所有棱的长度之和)
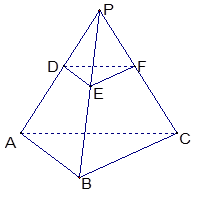
(1)求证:P-ABC为正四面体;
(2)棱PA上是否存在一点M,使得BM与面ABC所成的角为45°?若存在,求出点M的位置;若不存在,请说明理由。
(3)设棱台DEF-ABC的体积为V=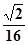 , 是否存在体积为V且各棱长均相等的平行六面体,使得它与棱台DEF-ABC有相同的棱长和,并且该平行六面体的一条侧棱与底面两条棱所成的角均为60°? 若存在,请具体构造出这样的一个平行六面体,并给出证明;若不存在,请说明理由.
, 是否存在体积为V且各棱长均相等的平行六面体,使得它与棱台DEF-ABC有相同的棱长和,并且该平行六面体的一条侧棱与底面两条棱所成的角均为60°? 若存在,请具体构造出这样的一个平行六面体,并给出证明;若不存在,请说明理由.