某批发站全年分批购入每台价值为3000 元的电脑共4000台，每批都购入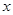
台，且每批均需付运费360元，储存电脑全年所付保管费与每批购入电脑的总价值（不含运费）成正比，若每批购入400台，则全年需用去运费和保管费共43600元，现在全年只有24000元资金可以用于支付这笔费用（运费和保管费），请问能否恰当安排进货数量使资金够用？写出你的结论，并说明理由．
相关试题
的不等式
（
，且
）.
.求分别满足下列条件的
的取值集合.
；
.
，求函数的定义域，判断函数
的奇偶性，并说明理由.
.
；
；
.
.推荐套卷
某批发站全年分批购入每台价值为3000 元的电脑共4000台，每批都购入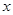台，且每批均需付运费360元，储存电脑全年所付保管费与每批购入电脑的总价值（不含运费）成正比，若每批购入400台，则全年需用去运费和保管费共43600元，现在全年只有24000元资金可以用于支付这笔费用（运费和保管费），请问能否恰当安排进货数量使资金够用？写出你的结论，并说明理由．
粤公网安备 44130202000953号