已知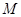 为抛物线
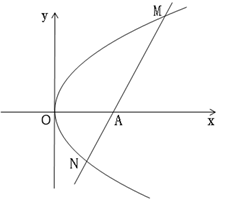
为抛物线 上一动点,
上一动点,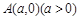 为其对称轴上一点,直线
为其对称轴上一点,直线 与抛物线的另一个交点为
与抛物线的另一个交点为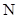 .当
.当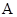 为抛物线的焦点且直线
为抛物线的焦点且直线 与其对称轴垂直时,△
与其对称轴垂直时,△ 的面积为
的面积为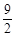 .
.
(1)求抛物线的标准方程;
(2)记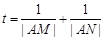 ,若
,若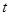 的值与
的值与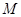 点位置无关,则称此时的点A为“稳定点”,试求出所有“稳
点位置无关,则称此时的点A为“稳定点”,试求出所有“稳
定点”,若没有,请说明理由.
相关知识点
推荐套卷
已知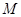 为抛物线
为抛物线 上一动点,
上一动点,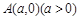 为其对称轴上一点,直线
为其对称轴上一点,直线 与抛物线的另一个交点为
与抛物线的另一个交点为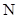 .当
.当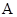 为抛物线的焦点且直线
为抛物线的焦点且直线 与其对称轴垂直时,△
与其对称轴垂直时,△ 的面积为
的面积为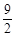 .
.
(1)求抛物线的标准方程;
(2)记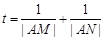 ,若
,若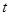 的值与
的值与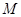 点位置无关,则称此时的点A为“稳定点”,试求出所有“稳
点位置无关,则称此时的点A为“稳定点”,试求出所有“稳
定点”,若没有,请说明理由.