已知数列 是递增的等比数列,满足
是递增的等比数列,满足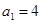 ,且
,且 是
是 .
.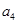 的等差中项,数列
的等差中项,数列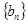 满足
满足 ,其前n项和为
,其前n项和为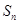 ,且
,且 .
.
(1)求数列 ,
,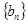 的通项公式;
的通项公式;
(2)数列 的前n项和为
的前n项和为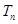 ,若不等式
,若不等式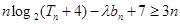 对一切
对一切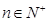 恒成立,求实数
恒成立,求实数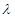 的取值范围.
的取值范围.
相关知识点
推荐套卷
已知数列 是递增的等比数列,满足
是递增的等比数列,满足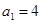 ,且
,且 是
是 .
.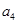 的等差中项,数列
的等差中项,数列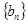 满足
满足 ,其前n项和为
,其前n项和为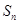 ,且
,且 .
.
(1)求数列 ,
,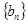 的通项公式;
的通项公式;
(2)数列 的前n项和为
的前n项和为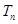 ,若不等式
,若不等式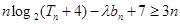 对一切
对一切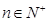 恒成立,求实数
恒成立,求实数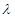 的取值范围.
的取值范围.