观察一列数:1、2、4、8、16、…我们发现,这一列数从第二项起,每一项与它前一项的比都等于2.一般地,如果一列数从第二项起,每一项与它前一项的比都等于同一个常数,这一列数就叫做等比数列,这个常数就叫做等比数列的公比.
(1)等比数列5、-15、45、…的第4项是_________.
(2)如果一列数 是等比数列,且公比为
是等比数列,且公比为 .那么有:
.那么有: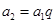 ,
, ,
, .则:
.则: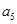 = .(用
= .(用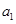 与
与 的式子表示)
的式子表示)
(3)一个等比数列的第2项是10,第4项是40,求它的公比.
观察一列数:1、2、4、8、16、…我们发现,这一列数从第二项起,每一项与它前一项的比都等于2.一般地,如果一列数从第二项起,每一项与它前一项的比都等于同一个常数,这一列数就叫做等比数列,这个常数就叫做等比数列的公比.
(1)等比数列5、-15、45、…的第4项是_________.
(2)如果一列数 是等比数列,且公比为
是等比数列,且公比为 .那么有:
.那么有: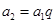 ,
, ,
, .则:
.则: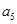 = .(用
= .(用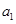 与
与 的式子表示)
的式子表示)
(3)一个等比数列的第2项是10,第4项是40,求它的公比.