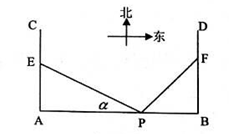
如图,在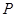 地正西方向
地正西方向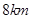 的
的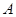 处和正东方向
处和正东方向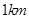 的
的 处各有一条正北方向的公路
处各有一条正北方向的公路 和
和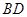 ,现计划在
,现计划在 和
和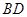 路边各维修一个物流中心
路边各维修一个物流中心 和
和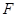 ,为缓解交通压力,决定修建两条互相垂直的公路
,为缓解交通压力,决定修建两条互相垂直的公路 和
和 ,设
,设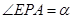
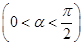 .
.
(1)为减少对周边区域的影响,试确定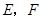 的位置,使
的位置,使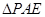 和
和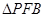 的面积之和最小;
的面积之和最小;
(2)为节省建设成本,试确定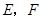 的位置,使
的位置,使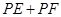 的值最小.
的值最小.
推荐套卷
如图,在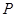 地正西方向
地正西方向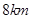 的
的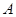 处和正东方向
处和正东方向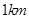 的
的 处各有一条正北方向的公路
处各有一条正北方向的公路 和
和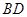 ,现计划在
,现计划在 和
和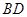 路边各维修一个物流中心
路边各维修一个物流中心 和
和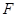 ,为缓解交通压力,决定修建两条互相垂直的公路
,为缓解交通压力,决定修建两条互相垂直的公路 和
和 ,设
,设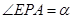
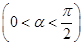 .
.
(1)为减少对周边区域的影响,试确定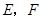 的位置,使
的位置,使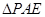 和
和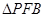 的面积之和最小;
的面积之和最小;
(2)为节省建设成本,试确定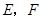 的位置,使
的位置,使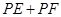 的值最小.
的值最小.